Spectral clustering

You can use Laplace spectra to cluster data. The idea is that the eigenvalues of the mesh’s Laplace spectrum can be embedded in a lower-dimensional space.

Data source for this notebooks: odedstein/meshes

import os
import glob
import napari_shape_odyssey as nso
import vedo
import numpy as np
import tqdm
from sklearn.manifold import TSNE
from sklearn.cluster import DBSCAN

import napari
import pandas as pd
import matplotlib.pyplot as plt

!git clone https://github.com/odedstein/meshes.git

Cloning into 'meshes'...
Updating files:  17% (17/96)
Updating files:  18% (18/96)
Updating files:  19% (19/96)
Updating files:  20% (20/96)
Updating files:  21% (21/96)
Updating files:  22% (22/96)
Updating files:  23% (23/96)
Updating files:  25% (24/96)
Updating files:  26% (25/96)
Updating files:  27% (26/96)
Updating files:  28% (27/96)
Updating files:  29% (28/96)
Updating files:  30% (29/96)
Updating files:  31% (30/96)
Updating files:  32% (31/96)
Updating files:  33% (32/96)
Updating files:  34% (33/96)
Updating files:  35% (34/96)
Updating files:  36% (35/96)
Updating files:  37% (36/96)
Updating files:  38% (37/96)
Updating files:  39% (38/96)
Updating files:  40% (39/96)
Updating files:  41% (40/96)
Updating files:  42% (41/96)
Updating files:  43% (42/96)
Updating files:  44% (43/96)
Updating files:  45% (44/96)
Updating files:  46% (45/96)
Updating files:  47% (46/96)
Updating files:  48% (47/96)
Updating files:  50% (48/96)
Updating files:  51% (49/96)
Updating files:  52% (50/96)
Updating files:  53% (51/96)
Updating files:  54% (52/96)
Updating files:  55% (53/96)
Updating files:  56% (54/96)
Updating files:  57% (55/96)
Updating files:  58% (56/96)
Updating files:  59% (57/96)
Updating files:  60% (58/96)
Updating files:  61% (59/96)
Updating files:  62% (60/96)
Updating files:  63% (61/96)
Updating files:  64% (62/96)
Updating files:  65% (63/96)
Updating files:  66% (64/96)
Updating files:  67% (65/96)
Updating files:  68% (66/96)
Updating files:  69% (67/96)
Updating files:  70% (68/96)
Updating files:  71% (69/96)
Updating files:  72% (70/96)
Updating files:  73% (71/96)
Updating files:  75% (72/96)
Updating files:  76% (73/96)
Updating files:  77% (74/96)
Updating files:  78% (75/96)
Updating files:  79% (76/96)
Updating files:  80% (77/96)
Updating files:  81% (78/96)
Updating files:  82% (79/96)
Updating files:  83% (80/96)
Updating files:  84% (81/96)
Updating files:  85% (82/96)
Updating files:  86% (83/96)
Updating files:  87% (84/96)
Updating files:  88% (85/96)
Updating files:  89% (86/96)
Updating files:  90% (87/96)
Updating files:  91% (88/96)
Updating files:  92% (89/96)
Updating files:  93% (90/96)
Updating files:  94% (91/96)
Updating files:  95% (92/96)
Updating files:  96% (93/96)
Updating files:  97% (94/96)
Updating files:  98% (95/96)
Updating files: 100% (96/96)
Updating files: 100% (96/96), done.

mesh_files = glob.glob(os.path.join('./meshes/**/*.obj'))

viewer = napari.Viewer()

Calculate spectra for every mesh

eigenvalues = []
eigenvectors = []
meshes = []
for file in tqdm.tqdm(mesh_files):
    # load and preprocess meshes
    mesh = vedo.load(file).triangulate().clean().decimate(n=5000)
    bounding_box_volume = np.prod(mesh.bounds()[1] - mesh.bounds()[0])
    mesh.scale(1 / bounding_box_volume)

    mesh_tuple = (mesh.points(), np.asarray(mesh.faces()))
    meshes.append(mesh_tuple)
    viewer.add_surface(mesh_tuple, name = os.path.basename(file))
    _eigenvectors, _eigenvalues = nso.spectral.shape_fingerprint(mesh_tuple, order = 20)

    eigenvalues.append(_eigenvalues)
    eigenvectors.append(_eigenvectors)

# stack eigenvalues into dataframe
eigenvalues_stack = np.stack(eigenvalues)
df = pd.DataFrame(eigenvalues_stack, columns = [f'lambda_{i}' for i in range(eigenvalues_stack.shape[1])])
df.head()

	lambda_0	lambda_1	lambda_2	lambda_3	lambda_4	lambda_5	lambda_6	lambda_7	lambda_8	lambda_9	lambda_10	lambda_11	lambda_12	lambda_13	lambda_14	lambda_15	lambda_16	lambda_17	lambda_18	lambda_19
0	-1.953646e-14	3.497411	4.534560	5.684497	9.985113	14.893090	22.529184	29.669639	30.541655	37.723114	41.284098	52.551030	58.486390	63.681724	64.850003	71.539644	78.696079	81.764765	95.658377	102.104163
1	1.382054e-14	3.497411	4.534560	5.684497	9.985113	14.893090	22.529184	29.669640	30.541655	37.723113	41.284097	52.551029	58.486391	63.681721	64.850001	71.539641	78.696077	81.764764	95.658375	102.104161
2	-2.596881e-15	0.683063	2.141403	4.065282	4.768848	4.828398	7.341017	7.398343	7.880799	10.123669	10.174560	11.785636	13.405222	14.186425	15.805213	16.056310	16.568611	18.689970	19.308144	21.437427
3	-3.480202e-14	7.361894	14.320784	29.855033	33.864331	38.218302	51.627914	55.100373	63.052792	71.963617	75.823578	91.888147	95.434760	99.987659	114.406247	123.437142	127.149471	140.136072	142.793974	153.672580
4	8.763823e-15	5.616643	7.917237	8.444330	16.360097	19.160159	20.802747	22.530132	30.035678	35.645911	37.769361	40.187326	41.239513	45.143890	48.583533	55.172578	60.318931	60.867925	64.006032	70.048105

Normalize spectra

# Fit a linear curve to every row of the dataframe and divide every value in the row by the slope of the curve

slope = []
intercept = []
for i in range(0, len(df)):
    x = np.arange(0, len(df.columns))
    y = df.iloc[i].values
    m, b = np.polyfit(x, y, 1)
    slope.append(m)
    intercept.append(b)

df = df.div(slope, axis=0)

Dimensionality reduction

embedder = TSNE(n_components=2)
X_embedded = embedder.fit_transform(df)

clusterer = DBSCAN(eps=0.25, min_samples=2)
clusterer.fit(X_embedded)

for idx, layer in enumerate(viewer.layers):
    mesh_tuple = list(layer.data)
    mesh_tuple[-1] *= clusterer.labels_[idx]
    viewer.layers[idx].data = tuple(mesh_tuple)
    viewer.layers[idx].colormap = 'tab10'
    viewer.layers[idx].contrast_limits = [-1, np.max(clusterer.labels_)]

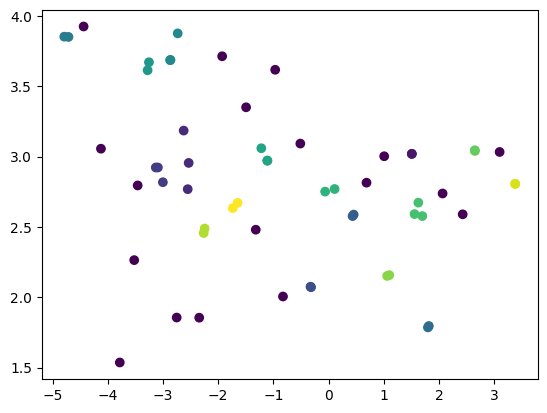
plt.scatter(X_embedded[:, 0], X_embedded[:, 1], c = clusterer.labels_)

<matplotlib.collections.PathCollection at 0x155abe32bb0>

for idx in np.argwhere(clusterer.labels_==4):
    viewer.add_surface(meshes[idx[0]], name = os.path.basename(mesh_files[idx[0]]))